6.3.4 Total Well-Mixed Greenhouse Gas Forcing Estimate
The radiative forcing due to all well-mixed greenhouse gases since pre-industrial
times was estimated to be 2.45 Wm-2 in the SAR with an uncertainty
of 15%. This is now altered to a radiative forcing of 2.43 Wm-2 with
an uncertainty of 10%, based on the range of model results and the discussion
of factors leading to uncertainties in the radiative forcing due to these greenhouse
gases. The uncertainty in the radiative forcing due to CO2 is estimated
to be smaller than for the other well-mixed greenhouse gases; less than 10%
(Section 6.3.1). For the CH4 forcing the main
uncertainty is connected to the radiative transfer code itself and is estimated
to be about 15% (Section 6.3.2). The uncertainty in N2O
(Section 6.3.2) is similar to that for CO2,
whereas the main uncertainties for halocarbons arise from the spectroscopic
data. The estimated uncertainty for halocarbons is 10 to 15% for the most frequently
studied species, but higher for some of the less investigated molecules (Section
6.3.3). A small increase in the concentrations of the
well-mixed greenhouse gases since the SAR has compensated for the reduction
in radiative forcing resulting from improved radiative transfer calculations.
The rate of increase in the well-mixed greenhouse gas concentrations, and thereby
the radiative forcing, has been smaller over the first half of the 1990s compared
to previous decades (see also Hansen et al., 1998). This is mainly a result
of reduced growth in CO2 and CH4 concentrations and smaller
increase or even reduction in the concentration of some of the halocarbons.
6.3.5 Simplified Expressions
IPCC (1990) used simplified analytical expressions for the well-mixed greenhouse
gases based in part on Hansen et al. (1988). With updates of the radiative forcing,
the simplified expressions need to be reconsidered, especially for CO2
and N2O. Shi (1992) investigated simplified expressions for the well-mixed
greenhouse gases and Hansen et al. (1988, 1998) presented a simplified expression
for CO2. Myhre et al. (1998b) used the previous IPCC expressions
with new constants, finding good agreement (within 5%) with high spectral resolution
radiative transfer calculations. The already well established and simple functional
forms of the expressions used in IPCC (1990), and their excellent agreement
with explicit radiative transfer calculations, are strong bases for their continued
usage, albeit with revised values of the constants, as listed in Table
6.2. Shi (1992) has suggested more physically based and accurate expressions
which account for (i) additional absorption bands that could yield a separate
functional form besides the one in IPCC (1990), and (ii) a better treatment
of the overlap between gases. WMO (1999) used a simplified expression for CO2
based on Hansen et al. (1988) and this simplified expression is used in the
calculations of GWP in Section 6.12. For CO2
the simplified expressions from Shi (1992) and Hansen et al. (1988) are also
listed alongside the IPCC (1990)-like expression for CO2 in Table
6.2. Compared to IPCC (1990) and the SAR and for similar changes in the
concentrations of well-mixed greenhouse gases, the improved simplified expressions
result in a 15% decrease in the estimate of the radiative forcing by CO2
(first row in Table 6.2), a 15% decrease in the case of
N2O, an increase of 10 to 15% in the case of CFC-11 and CFC-12, and
no change in the case of CH4.
| Table 6.2: Simplified expressions for calculation
of radiative forcing due to CO2, CH4, N2O,
and halocarbons. The first row for CO2 lists an expression with
a form similar to IPCC (1990) but with newer values of the constants. The
second row for CO2 is a more complete and updated expression
similar in form to that of Shi (1992). The third row expression for CO2
is from WMO (1999), based in turn on Hansen et al. (1988). |
 |
|
Trace gas
|
Simplified expression Radiative forcing,  F
(Wm-2) F
(Wm-2)
|
Constants
|
 |
| CO2 |
 F = F =  ln(C/C0) ln(C/C0) |
 = 5.35 = 5.35 |
| |
 F= F=  ln(C/C0)
+ ß ( ln(C/C0)
+ ß (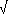 C - C - 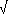 C0) C0) |
 = 4.841, ß =
0.0906 = 4.841, ß =
0.0906 |
| |
 F= F=  (g(C)–g(C0)) (g(C)–g(C0))
where g(C)= ln(1+1.2C+0.005C2 +1.4 x 10-6C3)
|
 = 3.35 = 3.35 |
 |
| CH4 |
 F= F=  ( (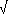 M
– M
– 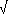 M0) –
(f(M,N0) – f(M0,N0)) M0) –
(f(M,N0) – f(M0,N0)) |
 = 0.036 = 0.036 |
 |
| N2O |
 F= F=  ( (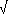 N
– N
– 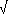 N0) – (f(M0,N)
– f(M0,N0)) N0) – (f(M0,N)
– f(M0,N0)) |
 = 0.12 = 0.12 |
 |
| CFC-11a |
 F= F=  (X
– X0) (X
– X0) |
 = 0.25 = 0.25 |
 |
| CFC-12 |
 F= F=  (X
– X0) (X
– X0) |
 = 0.32 = 0.32 |
 |